Ives–Stilwell experiment
The Ives–Stilwell experiment exploits the transverse Doppler effect (TDE). This was the first direct, quantitative confirmation of the time dilation factor. Together with the Michelson–Morley and Kennedy–Thorndike experiments, it forms one of the fundamental tests of special relativity theory.[1] Other tests confirming the relativistic Doppler effect, are the Mössbauer rotor experiment and modern Ives–Stilwell experiments. For other time dilation experiments in general, see Time dilation of moving particles. For other tests in general, see Tests of special relativity.
Contents |
Ives–Stilwell experiment
The TDE was described by Albert Einstein in his seminal 1905 paper.[2] Einstein subsequently suggested an experiment based on the measurement of the relative frequencies of light perceived as arriving from a light source in motion with respect to the observer. Herbert E. Ives and G. R. Stilwell (although they referred to time dilation as following from the "theory of Lorentz and Larmor") undertook the task of executing the experiment and they came up with a very clever way of separating the much smaller TDE from the much bigger longitudinal Doppler effect. The experiment was executed in 1938[3] and it was reprised multiple times (see, e.g.[4]). Similar experiments were conducted several times with increased precision, by Otting (1939),[5] Mandelberg et al. (1962),[6] Hasselkamp et al. (1979),[7]
Ives remarked, that it is nearly impossible to measure the transverse Doppler effect with respect to light rays emitted by canal rays, at right angles to the direction of motion of the canal rays (as it was considered earlier by Einstein), because the influence of the longitudinal effect can hardly be excluded. Therefore he developed a method, to observe the effect in the longitudinal direction of the canal rays' motion. If it is assumed that the speed of light is fixed with respect to the observer (“Classical Theory”), then the forward and rearward Doppler-shifted frequencies seen on a moving object will be f'/f = c/(c±v), where v is recession velocity. Under special relativity, the two frequencies will also include an additional “Lorentz factor” redshift correction.
When we invert these relationships so that they relate to wavelengths rather than frequencies, “Classical Theory” predicts redshifted and blueshifted wavelength values of 1+v/c and 1-v/c, so if all three wavelengths (redshifted, blueshifted and original) are marked on a linear scale, according to Classical Theory the three marks should be perfectly evenly spaced.
But if the light is shifted by special relativity's predictions, the additional Lorentz offset means that the two outer marks will be offset in the same direction with respect to the central mark.
Ives and Stilwell found that there was a significant offset of the centre of gravity of the three marks, and therefore the Doppler relationship was not that of "Classical Theory". This approach had two main advantages:
- didn't require us to commit to an exact value for the velocity involved (which might have been theory-dependent), and
- it didn't require an understanding or interpretation of angular aberration effects, as might have been required for the analysis of a "true" transverse test. A "true transverse test" has been run almost 40 years later, by Hasselkamp in 1979.[7]
Mössbauer rotor experiments
- Relativistic Doppler effect
A more precise confirmation of the relativistic Doppler effect was achieved by the Mössbauer rotor experiments. From a source in the middle of a rotating disk, gamma rays are being sent to a receiver at the rim (in some variations this scheme was reversed). Due to the rotation velocity of the receiver, the absorption frequency decreases if the transverse Doppler effect exists. This effect was actually observed using the Mössbauer effect. The maximal deviation from time dilation was 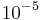 , thus the precision was much higher than that (
, thus the precision was much higher than that (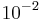 ) of the Ives–Stilwell experiments. Such experiments were performed by Hay et al. (1960),[8] Champeney et al. (1963, 1965),[9][10] Kündig (1963).[11]
) of the Ives–Stilwell experiments. Such experiments were performed by Hay et al. (1960),[8] Champeney et al. (1963, 1965),[9][10] Kündig (1963).[11]
- Isotropy of the speed of light
Moessbauer rotor experiments were also used to measure a possible anisotropy of the speed of light. That is, a possible aether wind should exert a disturbing influence on the absorption frequency. However, like in all other aether drift experiments (Michelson–Morley experiment), the result was negative, putting an upper limit to aether drift of 3–4 m/s. Experiments of that kind were performed by Champeney & Moon (1961),[12] Champeney et al. (1963)[13] and Turner & Hill (1964).[14]
Modern experiments
Fast moving clocks
A considerably higher precision has been achieved in modern variations of Ives–Stilwell experiments. In heavy ion storage rings, as the TSR at the MPIK, the Doppler shift of lithium ions traveling at high speeds is evaluated by using Saturated spectroscopy. Due to their frequencies emitted, these ions can be considered as optical atomic clocks of high precision.
| Author | Year | Maximum deviation from time dilation |
|---|---|---|
| Grieser et al.[15] | 1994 | 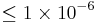 |
| Saathoff et al.[16] | 2003 | 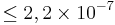 |
| Reinhardt et al.[17] | 2007 | 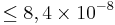 |
Slow moving clocks
Meanwhile, the measurement of time dilation at every day's speeds has been accomplished as well. For that purpose, Chou et al. (2010) used aluminium ions, moving within a 75 m long, phase-stabilized optical fiber. These optical atomic clocks emitted frequencies of a certain frequency, and the sensitivity of this experiment was 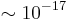 . Therefore, it was possible to measure a frequency shift due to time dilation of
. Therefore, it was possible to measure a frequency shift due to time dilation of 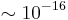 at speeds below 36 km/h (< 10 m/s), by comparison of the rates of moving and resting clocks.[18]
at speeds below 36 km/h (< 10 m/s), by comparison of the rates of moving and resting clocks.[18]
References
- ^ Robertson, H. P. (1949). "Postulate versus Observation in the Special Theory of Relativity". Reviews of Modern Physics 21 (3): 378–382. Bibcode 1949RvMP...21..378R. doi:10.1103/RevModPhys.21.378.
- ^ Einstein, Albert (1905). "Zur Elektrodynamik bewegter Körper". Annalen der Physik 322 (10): 891–921. Bibcode 1905AnP...322..891E. doi:10.1002/andp.19053221004. English translation: ‘On the Electrodynamics of Moving Bodies’
- ^ Ives, H. E.; Stilwell, G. R. (1938). "An experimental study of the rate of a moving atomic clock". Journal of the Optical Society of America 28 (7): 215. Bibcode 1938JOSA...28..215I. doi:10.1364/JOSA.28.000215.
- ^ Ives, H. E.; Stilwell, G. R. (1941). "An experimental study of the rate of a moving atomic clock. II". Journal of the Optical Society of America 31 (5): 369. Bibcode 1941JOSA...31..369I. doi:10.1364/JOSA.31.000369.
- ^ Otting, G. (1939). "Der quadratische Dopplereffekt". Physikalische Zeitschrift 40: 681–687.
- ^ Mandelberg, Hirsch I.; Witten, Louis (1962). "Experimental verification of the relativistic doppler effect". Journal of the Optical Society of America 52 (5): 529. Bibcode 1962JOSA...52..529M.
- ^ a b Hasselkamp, D.; E. Mondry, A. Scharmann (1979-06-01). "Direct observation of the transversal Doppler-shift". Zeitschrift für Physik A 289 (2): 151–155. Bibcode 1979ZPhyA.289..151H. doi:10.1007/BF01435932.
- ^ Hay, H. J.; Schiffer, J. P.; Cranshaw, T. E.; Egelstaff, P. A. (1960). "Measurement of the Red Shift in an Accelerated System Using the Mössbauer Effect in Fe57". Physical Review Letters 4 (4): 165–166. Bibcode 1960PhRvL...4..165H. doi:10.1103/PhysRevLett.4.165.
- ^ Champeney, D. C.; Isaak, G. R.; Khan, A. M. (1963). "Measurement of Relativistic Time Dilatation using the Mössbauer Effect". Nature 198 (4886): 1186–1187. doi:10.1038/1981186b0.
- ^ Champeney, D. C.; Isaak, G. R.; Khan, A. M. (1965). "A time dilatation experiment based on the Mössbauer effect". Proceedings of the Physical Society 85 (3): 583–593. doi:10.1088/0370-1328/85/3/317.
- ^ Kündig, Walter (1963). "Measurement of the Transverse Doppler Effect in an Accelerated System". Physical Review 129 (6): 2371–2375. doi:10.1103/PhysRev.129.2371.
- ^ Champeney, D. C.; Moon, P. B. (1961). "Absence of Doppler Shift for Gamma Ray Source and Detector on Same Circular Orbit". Proceedings of the Physical Society 77 (2): 350–352. doi:10.1088/0370-1328/77/2/318.
- ^ Champeney, D. C.; Isaak, G. R.; Khan, A. M. (1963). "An 'aether drift' experiment based on the Mössbauer effect". Physics Letters 7 (4): 241–243. doi:10.1016/0031-9163(63)90312-3.
- ^ Turner, K. C.; Hill, H. A. (1964). "New Experimental Limit on Velocity-Dependent Interactions of Clocks and Distant Matter". Physical Review 134 (1B): 252–256. doi:10.1103/PhysRev.134.B252.
- ^ Grieser, R.; Klein, R.; Huber, G.; Dickopf, S.; Klaft, I.; Knobloch, P.; Merz, P.; Albrecht, F.; Grieser, M.; Habs, D.; Schwalm, D.; Kühl, T. (1994). "A test of special relativity with stored lithium ions". Applied Physics B Lasers and Optics 59 (2): 127–133. doi:10.1007/BF01081163.
- ^ Saathoff, G.; Karpuk, S.; Eisenbarth, U.; Huber, G.; Krohn, S.; Horta, R. Muñoz; Reinhardt, S.; Schwalm, D.; Wolf, A.; Gwinner, G. (2003). "Improved Test of Time Dilation in Special Relativity". Phys. Rev. Lett. 91 (19): 190403. Bibcode 2003PhRvL..91s0403S. doi:10.1103/PhysRevLett.91.190403.
- ^ Reinhardt, S.; Saathoff, G.; Buhr, H.; Carlson, L. A.; Wolf, A.; Schwalm, D.; Karpuk, S.; Novotny, C.; Huber, G.; Zimmermann, M.; Holzwarth, R.; Udem, T.; Hänsch, T. W.; Gwinner, G. (2007). "Test of relativistic time dilation with fast optical atomic clocks at different velocities". Nature Physics 3 (12): 861–864. Bibcode 2007NatPh...3..861R. doi:10.1038/nphys778.
- ^ Chou, C. W.; Hume, D. B.; Rosenband, T.; Wineland, D. J. (2010). "Optical Clocks and Relativity". Science 329 (5999): 1630–1633. Bibcode 2010Sci...329.1630C. doi:10.1126/science.1192720. PMID 20929843.
External links
- Roberts, T; Schleif, S; Dlugosz, JM (ed.) (2007). "What is the experimental basis of Special Relativity?". Usenet Physics FAQ. University of California, Riverside. http://math.ucr.edu/home/baez/physics/Relativity/SR/experiments.html.
- Modern Reenactments of Relativity Tests
- M Moriconi, 2006, Special theory of relativity through the Doppler effect
- Warp Special Relativity Simulator Computer program demonstrating the relativistic doppler effect.
- The Doppler Effect at MathPages
|
|||||||||||||||||||||||